miércoles, 19 de noviembre de 2008
martes, 21 de octubre de 2008
Errores científicos de la Biblia
Título: Errores científicos de la BibliaAutor: Emilio Ferrière
Año: 1904
Páginas: 424
Argumento: Es un ensayo de crítica al Concilio de Trento y a la asunción literal de los contenidos de la Biblia. Se exponen las principales discrepancias entre los resultados científicos más "actuales" y la interpretación bíblica, y se propugna la reinterpretación de los textos sagrados, como se hace con otros documentos históricos.
Valoración: Hace ya algún tiempo, tuve la fortuna de encontrarme con este "bicho raro" en la tienda de antigüedades de mi tía. Lo primero que llama la atención al comenzar la lectura es la formalidad típica del hombre de ciencia de aquella época, que quien haya leído libros de matemáticas "antiguos" reconocerá enseguida. Se trata de una formalidad en los conceptos, y no en las formas, conforme a la costumbre de utilizar el lenguaje más natural y comprensible aun en los textos de carácter más técnico.
El libro se divide en una introducción y varias partes. La introducción explica de manera concisa pero completa todas las fases de la formación de la Biblia, explicando el origen de cada uno de los textos que la componen. A continuación hay 8 partes, en cada una de las cuales se analiza un aspecto de la realidad, su interpretación científica y su interpretación "literal" bíblica. Estas 8 partes son: cosmogonía (creación del mundo), astronomía (constitución, formación y disposición de los astros), metereología (especialmente el diluvio universal), zoología (organización del reino animal), botánica (clasificación de los vegetales), geología (formación de la superficie terrestre), fisiología (condiciones vitales de las plantas y de los animales) y física (especialmente el arco iris).
Al margen del interés que cada uno tenga en aprender o leer acerca de la Biblia y sus orígenes, recomendaría la lectura de este libro para comprender el pensamiento científico que existía hace un siglo (no muy lejano al actual). Además, las explicaciones científicas son bastante extensas y sencillas de comprender, de modo que es una oportunidad para conocer, por ejemplo, la teoría de Laplace acerca de la formación de los planetas. Por otro lado, personalmente estoy completamente de acuerdo (ya lo estaba antes de descubrir el libro) con el autor en su defensa de la exégesis de la Biblia y su crítica al Santo Concilio de Trento. Y que el título no dé lugar a malos entendidos: no se trata de un científico criticando a la Biblia, sino de un creyente (se nota en sus palabras) que quiere una Biblia renovada y revalorizada, acorde con las cosas que se van aprendiendo de ella y del mundo.
lunes, 20 de octubre de 2008
Planilandia
En 1884 Edwin Abbott Abbott escribía "Planilandia, un romance en muchas dimensiones", novela aún popular hoy en día entre estudiantes de matemáticas, informática, física y algún otro tipo de frikis. La historia es narrada en primera persona por un cuadrado que, a veces en sueños a veces no, viaja a mundos de dimensiones diferentes a la suya (él vive en planilandia, en 2 dimensiones). Más allá de lo absurdo que pueda resultar el argumento, las disquisiciones metafísicas del cuadrado acerca de los mundos de menos y más dimensiones que el suyo presentan un claro paralelismo con las que podemos tener en nuestro mundo de 3 dimensiones; la metáfora está servida, y es muy útil para ayudarnos a entender mejor esto de las 3 dimensiones.
Hace algún tiempo, el Doctor Quantum nos explicaba el experimento de la doble ranura. Veamos qué nos puede contar acerca de Planilandia:
Hace algún tiempo, el Doctor Quantum nos explicaba el experimento de la doble ranura. Veamos qué nos puede contar acerca de Planilandia:
domingo, 19 de octubre de 2008
jueves, 16 de octubre de 2008
Sólo sé que ... no quiero saberlo
"Hay muchas cosas que no quiero saber. La sabiduría marca límites hasta al conocimiento."
Friedrich Nietzsche
Friedrich Nietzsche
miércoles, 15 de octubre de 2008
Diferencias finitas
El otro día leí en Gaussianos que
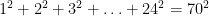
Además dicen que es la única suma de cuadrados de los n primeros naturales consecutivos que da como resultado un cuadrado perfecto. Como dicen ellos, una curiosidad curiosa.
El caso es que a mí me pica la curiosidad y en estos casos suelo preguntarme: ¿será cierto? Así que vamos a intentar demostrarlo. Para ello, lo primero es encontrar una fórmula que nos diga cuál es la suma de los n primeros números enteros. Una fórmula f(n) que para los valores de n 0,1,2,3,... nos dé los resultados 1,5,14,30,...
No es la primera vez que explico un método para calcular sumas, aunque aquél habría que generalizarlo un poco para adaptarlo a este problema (como bien entenderán quienes lo hayan utilizado para resolver el problema difícil de aquellos acertijos que un día puse). Para este tipo de problemas, existe otro método más útil, al que yo llamo, porque otros lo han bautizado antes, método de diferencias finitas.
Vamos a intentar explicarlo de la manera más sencilla posible. Yo intento "deducir" una fórmula polinómica para la sucesión:
1 5 14 30 55 91 ...
Lo que voy a hacer es restar a cada número el anterior; en este caso 5-1, 14-5, 30-14,... para conseguir una nueva sucesión, que evidentemente será la de los cuadrados perfectos, pues sumándolos es como creé la anterior:
4 9 16 25 36 ...
Y continúo procediendo de la misma manera hasta llegar a una sucesión con todos los términos iguales:
1 5 14 30 55 91
4 9 16 25 36
5 7 9 11
2 2 2
Como vemos, hemos necesitado 3 pasos para llegar a la secuencia de números iguales. Esto quiero decir que nuestra función polinómica va a ser de grado 3. Ahora para construirla utilizaremos sólo los primeros coeficientes obtenidos en las anteriores sucesiones, es decir, los números 1, 4, 5 y 2, y en ese orden.
Si a estos coeficientes los llamamos a, b, c, d, etc. (aquí tenemos 4 pero podrían ser más), se verifica (este es el verdadero método), que la función buscada debe ser:
a + b·n + c·n·(n-1)/2 + d·n·(n-1)·(n-2)/(2·3) + ...
donde el k-ésimo término de la suma es el correspondiente coeficiente multiplicado por n·(n-1)·(n-2)·... [k-1 factores] y dividido por el factorial de (k-1). De este modo es "fácil de recordar".
Aplicado a nuestro problema concreto, tenemos que a=1, b=4, c=5 y d=2, por lo que:
f(n) = 1 + 4n + 5n(n-1)/2 + n(n-1)(n-2)/3 = ... = (2n^3 + 9n^2 + 13n + 6)/6
Si aplicamos la fórmula obtenida (tened en cuenta que el primer valor de n es 0), comprobamos que:
f(0) = 1
f(1) = 5
f(2) = 14
f(3) = 30
...
La suma de los 24 primeros números enteros debe ser f(23) = 4900, que efectivamente es el cuadrado de 70, con lo que hemos verificado la igualdad sin hacer todos los cuadrados y las sumas (apenas hemos hecho unas restas para sacar la fórmula).
Lo que nos quedaría ahora es demostrar que f(23) es el único valor cuadrado perfecto que toma la función f así definida. ¿A alguien se le ocurre cómo?
Además dicen que es la única suma de cuadrados de los n primeros naturales consecutivos que da como resultado un cuadrado perfecto. Como dicen ellos, una curiosidad curiosa.
El caso es que a mí me pica la curiosidad y en estos casos suelo preguntarme: ¿será cierto? Así que vamos a intentar demostrarlo. Para ello, lo primero es encontrar una fórmula que nos diga cuál es la suma de los n primeros números enteros. Una fórmula f(n) que para los valores de n 0,1,2,3,... nos dé los resultados 1,5,14,30,...
No es la primera vez que explico un método para calcular sumas, aunque aquél habría que generalizarlo un poco para adaptarlo a este problema (como bien entenderán quienes lo hayan utilizado para resolver el problema difícil de aquellos acertijos que un día puse). Para este tipo de problemas, existe otro método más útil, al que yo llamo, porque otros lo han bautizado antes, método de diferencias finitas.
Vamos a intentar explicarlo de la manera más sencilla posible. Yo intento "deducir" una fórmula polinómica para la sucesión:
1 5 14 30 55 91 ...
Lo que voy a hacer es restar a cada número el anterior; en este caso 5-1, 14-5, 30-14,... para conseguir una nueva sucesión, que evidentemente será la de los cuadrados perfectos, pues sumándolos es como creé la anterior:
4 9 16 25 36 ...
Y continúo procediendo de la misma manera hasta llegar a una sucesión con todos los términos iguales:
1 5 14 30 55 91
4 9 16 25 36
5 7 9 11
2 2 2
Como vemos, hemos necesitado 3 pasos para llegar a la secuencia de números iguales. Esto quiero decir que nuestra función polinómica va a ser de grado 3. Ahora para construirla utilizaremos sólo los primeros coeficientes obtenidos en las anteriores sucesiones, es decir, los números 1, 4, 5 y 2, y en ese orden.
Si a estos coeficientes los llamamos a, b, c, d, etc. (aquí tenemos 4 pero podrían ser más), se verifica (este es el verdadero método), que la función buscada debe ser:
a + b·n + c·n·(n-1)/2 + d·n·(n-1)·(n-2)/(2·3) + ...
donde el k-ésimo término de la suma es el correspondiente coeficiente multiplicado por n·(n-1)·(n-2)·... [k-1 factores] y dividido por el factorial de (k-1). De este modo es "fácil de recordar".
Aplicado a nuestro problema concreto, tenemos que a=1, b=4, c=5 y d=2, por lo que:
f(n) = 1 + 4n + 5n(n-1)/2 + n(n-1)(n-2)/3 = ... = (2n^3 + 9n^2 + 13n + 6)/6
Si aplicamos la fórmula obtenida (tened en cuenta que el primer valor de n es 0), comprobamos que:
f(0) = 1
f(1) = 5
f(2) = 14
f(3) = 30
...
La suma de los 24 primeros números enteros debe ser f(23) = 4900, que efectivamente es el cuadrado de 70, con lo que hemos verificado la igualdad sin hacer todos los cuadrados y las sumas (apenas hemos hecho unas restas para sacar la fórmula).
Lo que nos quedaría ahora es demostrar que f(23) es el único valor cuadrado perfecto que toma la función f así definida. ¿A alguien se le ocurre cómo?
domingo, 12 de octubre de 2008
Proyecto 10 al 100
¿Tienes alguna idea genial para cambiar el mundo, para mejorar la calidad de vida de las personas, lograr un ecosistema más ecológico, para que las personas tengan más oportunidades o mejor comunicación y preservación de sus culturas? Pues bien, te queda una semana (hasta el lunes 20 de octubre) para participar en el concurso de ideas que Google ha lanzado bajo el nombre 10 elevado a 100.
La pregunta fundamental (por lo que una idea valdrá más que otras) es: ¿A cuánta gente puede ayudar tu idea?
El siguiente vídeo es muy explicativo:
Enviar una idea resulta muy sencillo, pues sólo hay que cubrir un formulario no muy extenso. Después de que un grupo de expertos de Google revise todas las ideas, se seleccionarán y publicarán 100 para que el público las vote a partir del 27 de enero de 2009. A principios de febrero se conocerán las 5 ideas ganadoras. Google destinará 10 millones de dólares a la ejecución de las 5 mejores ideas, habiendo seleccionado también mediante concurso a la empresa que se dedicará a su desarrollo. El premio para el autor de la idea ganadora es buen karma.
La pregunta fundamental (por lo que una idea valdrá más que otras) es: ¿A cuánta gente puede ayudar tu idea?
El siguiente vídeo es muy explicativo:
Enviar una idea resulta muy sencillo, pues sólo hay que cubrir un formulario no muy extenso. Después de que un grupo de expertos de Google revise todas las ideas, se seleccionarán y publicarán 100 para que el público las vote a partir del 27 de enero de 2009. A principios de febrero se conocerán las 5 ideas ganadoras. Google destinará 10 millones de dólares a la ejecución de las 5 mejores ideas, habiendo seleccionado también mediante concurso a la empresa que se dedicará a su desarrollo. El premio para el autor de la idea ganadora es buen karma.
jueves, 9 de octubre de 2008
miércoles, 8 de octubre de 2008
Concurso de viñetas sobre tecnología
El próximo lunes se cierra el plazo para presentar viñetas al VIII Concurso Internacional de Humor Gráfico de Barakaldo "Nuevas Tecnologías".
Si tienes o puedes tener una viñeta graciosa sobre el impacto de las nuevas tecnologías en nuestra vida cotidiana, lo único que tienes que hacer es enviarla antes del lunes por correo electrónico a hermesbarakaldo@barakaldo.org
La imagen debe tener una resolución mínima de 72 píxeles por pulgada y un tamaño máximo de 800x600 píxeles, así como ser enviada en formato JPG adjunto al correo en el que se especificarán los datos personales: nombre, apellido, dirección, fecha de nacimiento, DNI y teléfono de contacto.
Todo el mundo puede participar y se darán cinco premios en dinero, que van desde los 500 hasta los 1500 euros.
Si tienes o puedes tener una viñeta graciosa sobre el impacto de las nuevas tecnologías en nuestra vida cotidiana, lo único que tienes que hacer es enviarla antes del lunes por correo electrónico a hermesbarakaldo@barakaldo.org
La imagen debe tener una resolución mínima de 72 píxeles por pulgada y un tamaño máximo de 800x600 píxeles, así como ser enviada en formato JPG adjunto al correo en el que se especificarán los datos personales: nombre, apellido, dirección, fecha de nacimiento, DNI y teléfono de contacto.
Todo el mundo puede participar y se darán cinco premios en dinero, que van desde los 500 hasta los 1500 euros.
martes, 7 de octubre de 2008
Aprender fuera de la ciencia, eso es lo difícil
"El aspecto más triste de la vida actual es que la ciencia gana en conocimiento más rápidamente que la sociedad en sabiduría"
Isaac Asimov
Isaac Asimov
lunes, 6 de octubre de 2008
Cómo dibujar chicas (y manga, anime, cómic,...)
Idrawgirls.com es un fantástico compendio de más de 200 vídeos tutoriales gratuitos que explican cómo dibujar y pintar, normalmente en Photoshop, chicas (y otras criaturas) al estilo manga, anime o cómic. El blog ha sido creado por XIA el año pasado, según dice, para automotivarse a crear más y mejor arte. Y lo cierto es que arte no le falta.
La iniciativa de XIA, del tipo "si quieres aprender enseña", creo que es un ejemplo más de lo productivo que puede resultar para uno mismo el esfuerzo de intentar compartir lo que sabe.
En cuanto a lo que podemos aprender el resto de mortales/artistas-aficionados, en mi opinión para seguir los tutoriales se requiere un nivel mínimo de conocimientos de Photoshop o de conocimientos de dibujo. Es decir, si ya sabes dibujar te serán muy útiles para aprender a uilizar el Photoshop, mientras que si sabes usarlo pero no sabes dibujar, puedes aprender distintos "trucos" básicos del artista, en qué orden dibujar las cosas, qué referencias utilizar o cómo aprovechar las capas y efectos de Photoshop para trabajar en las distintas fases de un boceto.
Si eres de los que, como yo, no sabes dibujar demasiado bien ni has usado mucho el Photoshop, el camino será más largo, ya que cada vídeo contendrá "demasiada sabiduría" junta para una primera lección, pero aprender está garantizado. Eso sí, atendiendo a peticiones de los visitantes, desde el pasado mayo XIA ha colgado algunos tutoriales de uso básico de Photoshop, que sin duda nos facilitará las cosas a los que estamos empezando.
La iniciativa de XIA, del tipo "si quieres aprender enseña", creo que es un ejemplo más de lo productivo que puede resultar para uno mismo el esfuerzo de intentar compartir lo que sabe.
En cuanto a lo que podemos aprender el resto de mortales/artistas-aficionados, en mi opinión para seguir los tutoriales se requiere un nivel mínimo de conocimientos de Photoshop o de conocimientos de dibujo. Es decir, si ya sabes dibujar te serán muy útiles para aprender a uilizar el Photoshop, mientras que si sabes usarlo pero no sabes dibujar, puedes aprender distintos "trucos" básicos del artista, en qué orden dibujar las cosas, qué referencias utilizar o cómo aprovechar las capas y efectos de Photoshop para trabajar en las distintas fases de un boceto.
Si eres de los que, como yo, no sabes dibujar demasiado bien ni has usado mucho el Photoshop, el camino será más largo, ya que cada vídeo contendrá "demasiada sabiduría" junta para una primera lección, pero aprender está garantizado. Eso sí, atendiendo a peticiones de los visitantes, desde el pasado mayo XIA ha colgado algunos tutoriales de uso básico de Photoshop, que sin duda nos facilitará las cosas a los que estamos empezando.
domingo, 5 de octubre de 2008
Campeón de España
David Lariño se ha proclamado ayer campeón de España absoluto de ajedrez. ¡Enhorabuena, David!Para aquellos que no le conozcáis, me gustaría advertiros que algunos medios (más de uno y más de dos) afirman erróneamente que David es navarro. Los que le conocemos un poco (yo sólo tuve ocasión de verle jugar en el I Memorial Xosé Henrique Rodríguez Peña), sabemos que David Lariño es gallego. Concretamente de Esteiro.
La confusión de los medios se debe a que el pasado año David se ha unido al equipo navarro Santa Ana de Tudela, por lo que en los resultados del campeonato que da la Federación, figura como jugador federado por Navarra. En el poco tiempo que lleva federado por Navarra, no es la primera vez que se produce esta confusión.
El efecto curioso que está ocurriendo es que el triunfo se está celebrando "por duplicado" estos días, ya que los medios de Navarra y de Galicia se están llenando de titulares llenos de orgullo por el campeón.
En cualquier caso, un logro excepcional y admirable el de David. ¡Felicidades, campeón!
Mr Pip (segunda parte)
Al fin he tenido tiempo para terminar de leerlo.Definitivamente, como ya anticipaba, un libro muy recomendable.
Para no pisar nada, sólo diré que la historia atrapa tanto al lector que en el final de la misma, a pesar de continuar con las cálidas frases abundantes en lirismo, parecen sucederse los acontecimientos como si se tratase de un tren que alcanza su máxima velocidad sin poder detenerse; del mismo modo, una vez se enfilan los últimos capítulos es imposible despegarse del libro. Y lo digo porque, por elegir el peor momento para acabar de leerlo, tuve que intentar interrumpir la lectura para hacer otras cosas... pero no fui capaz. Es posarlo cerrado encima de la mesa con el marcapáginas cerca de la última página y pensar... "¡diablos, tengo que ver cómo acaba!".
De las muchas moralejas que se pueden extraer, yo me quedo con esta: "Lee".
Sí, en cierto modo es una metamoraleja, ya que una de las cosas que nos enseña este libro es el poder de la lectura y de la imaginación de cada uno. A Matilda, la protagonista, leer puede haberle salvado la vida, pero no en el sentido literal y físico de la palabra, sino en el sentido más espiritual, en el sentido en que nos la puede salvar a todos. Y ya no desvelo más de la historia; que cada uno la descubra por sí mismo ;-)
domingo, 21 de septiembre de 2008
Ooooooh
Parece que el fin del mundo ha sido aplazado por el momento.
Una fuga de helio líquido producida ayer en el LHC obligará a mantenerlo parado y en reparaciones durante dos meses. Si es que así no hay manera.
Si no te fías de que el LHC pueda acabar con el mundo en tiempo y forma siempre puedes consultar los planos técnicos detallados (¡y con ejemplos!) para construirte tu propia versión.
Una fuga de helio líquido producida ayer en el LHC obligará a mantenerlo parado y en reparaciones durante dos meses. Si es que así no hay manera.
Si no te fías de que el LHC pueda acabar con el mundo en tiempo y forma siempre puedes consultar los planos técnicos detallados (¡y con ejemplos!) para construirte tu propia versión.
miércoles, 17 de septiembre de 2008
Stephen Hawking en Santiago de Compostela
El ilustre experto en agujeros negros, ahora que está de moda, Stephen Hawking, recibirá la semana que viene el Premio Fonseca 2008 de divulgación científica en la capital gallega. Para aquellos que se puedan acercar, este es el "programa de fiestas":
- lunes 22: llegada a Santiago
- martes 23: inauguración de una placa conmemorativa en el Parque de San Lázaro, y realización de un pequeño tramo del Camino de Santiago, hasta la plaza del Obradoiro, seguido de una visita a la Catedral
- miércoles 24: charla con investigadores de la Facultad de Física
- viernes 26: presentación de los libros "La clave secreta del Universo" y "Una brevísima historia del tiempo", en el Instituto de Bachillerato Rosalía de Castro
- sábado 27: entrega del Premio Fonseca, en el Palacio de Congresos y Exposiciones de Galicia
martes, 16 de septiembre de 2008
Libertad mental
El hombre libre es el que comprende que es dueño de su vida pero no de su existencia.
lunes, 15 de septiembre de 2008
Dios existe
Dicen que el número de átomos en el Universo se sitúa en torno a 10 elevado a 80. Imaginemos que tenemos 10 elevado a 80 billetes de lotería diferentes (cada uno podría tener, por ejemplo, un número de 80 dígitos decimales) y le damos uno a cada átomo. Estaremos de acuerdo en que la probabilidad de que a un átomo "le toque la lotería" es de 1 entre 10 elevado a 80. Sin duda, sería la lotería más difícil de ganar, pues resulta complicado imaginar algo más improbable que eso.
Pues bien, vamos a imaginarlo: pensad en 30000 dados distribuidos en un rectángulo de 200 x 300 dados, adyacentes entre sí de forma que no dejen huecos entre ellos. Cada uno de ellos ha sido lanzado, de forma que muestra un número de puntos entre 1 y 6, con probabilidad 1/6 cada cara. ¿Cuál es la probabilidad de que los puntos que quedan a la vista formen en conjunto un rostro conocido? Alguien ha hecho el cálculo, y es de aproximadamente 1 entre 10 elevado a 23344.
¿Os parece improbable? Pues yo me pregunto... si asumimos que Dios no existe y todo lo que conocemos (incluídos nosotros mismos) es producto del azar, ¿cuál es la probabilidad de que la materia dispersa originariamente en el universo se agrupe de manera adecuada formando planetas, al menos uno de los cuales da origen a la vida que conocemos, y que en dicho planeta tras muchos años de evolución aparezca una especie inteligente de la cual un individuo llamado Einstein pose para una foto echando la lengua, y que años después otros individuos de la misma especie (creados por el azar, no lo olvidemos, luego sus creaciones también serán productos del azar) construyan una matriz de 30000 dados con el rostro de Einstein echando la lengua?
Pues ha sucedido:
Lo que nos lleva a preguntarnos: ¿cómo puede haber sucedido algo tan improbable? "Sólo" se me ocurren 3 explicaciones posibles:
- Alguien ha pulsado el botón de improbabilidad infinita.
- No todo es producto del azar: Dios existe.
- Existen infinitos Universos como el nuestro.
Pero si el número de universos fuese infinito, ¿por qué no llamar Dios al infinito?
Ahí queda eso.
Las mejores vistas de Ourense
Dicen que las mejores vistas de la ciudad de Ourense son las que hay desde el Seminario, pero en mi opinión son más fabulosas las que se consiguen desde la parte del Montealegre más cercana a la ciudad (Cruz Alta).
A diferencia del monte donde está el Seminario, este monte está completamente pegado a la ciudad, y tiene una preciosa y gran piedra digna del mismo Rey León donde te puedes sentar y literalmente tener la ciudad a tus pies.
A diferencia del monte donde está el Seminario, este monte está completamente pegado a la ciudad, y tiene una preciosa y gran piedra digna del mismo Rey León donde te puedes sentar y literalmente tener la ciudad a tus pies.
sábado, 13 de septiembre de 2008
Acertijos II
Fácil: ¿Qué día es hoy?
Medio: El triangulo de Sierpinski es una figura fractal, que se obtiene a partir de un triangulo equilátero, "eliminando" de él en primer lugar un triángulo central equivalente a un cuarto de su área y continuando el proceso de manera iterativa en cada uno de los triángulos resultantes:
Si llevamos el proceso al infinito, ¿qué proporción del triángulo original habremos eliminado?
Difícil: Demuestra que si x es el doble de la suma de los n primeros números naturales, entonces la expresión
da como resultado n+1.
Medio: El triangulo de Sierpinski es una figura fractal, que se obtiene a partir de un triangulo equilátero, "eliminando" de él en primer lugar un triángulo central equivalente a un cuarto de su área y continuando el proceso de manera iterativa en cada uno de los triángulos resultantes:
Si llevamos el proceso al infinito, ¿qué proporción del triángulo original habremos eliminado?Difícil: Demuestra que si x es el doble de la suma de los n primeros números naturales, entonces la expresión
da como resultado n+1.
El mundo sigue en pie, de momento...
El pasado miércoles, como todos sabréis, se ha puesto en funcionamiento el LHC, esa "cosa" que puede que acabe con el mundo. Evidentemente el mundo, tal como lo conocíamos, no se ha acabado, ni está planeado que lo haga (a causa del LHC) antes de finales de octubre, cuando realmente se comiencen a hacer colisiones.
Mientras algunos personajes relevantes hacen sus apuestas, otros se preocupan en ofrecernos respuesta a nuetras grandes preocupaciones, e incluso hay quienes se muestran excesivamente optimistas.
En cualquier caso, mientras todavía tengamos tiempo, podemos elaborar hipótesis acerca de por qué hemos llegado a esto... ¿Será que todos esos agujeros negros que hay por ahí son lo que queda de civilizaciones que apretaron el botón de un LHC? Gaussianos nos ofrece una interesante teoría al respecto.
Fuentes:
Microsiervos 1, 2, 3 y 4
Gaussianos
Mientras algunos personajes relevantes hacen sus apuestas, otros se preocupan en ofrecernos respuesta a nuetras grandes preocupaciones, e incluso hay quienes se muestran excesivamente optimistas.
En cualquier caso, mientras todavía tengamos tiempo, podemos elaborar hipótesis acerca de por qué hemos llegado a esto... ¿Será que todos esos agujeros negros que hay por ahí son lo que queda de civilizaciones que apretaron el botón de un LHC? Gaussianos nos ofrece una interesante teoría al respecto.
Pero no os preocupéis, para estar más tranquilos siempre tenemos a nuestra disposición estas webcam que retransmiten en directo el estado del experimento. No dejéis de visitar el enlace.
Fuentes:
Microsiervos 1, 2, 3 y 4
Gaussianos
Erasmus Café
Cuando estuve en Salamanca el pasado fin de semana tuve ocasión de conocer una cafetería/restaurante realmente muy recomendable: Erasmus Café.
Está bastante cerca de la Plaza Mayor, y tiene una decoración soberbia (paredes empapeladas con partituras, bicicletas colgando del techo, cuadros, chapas, monedas, ...); además el trato es muy amable. Los platos, sin ser demasiado caros, son abundantes y muy bien preparados.
Además, en su página web se puede enterar uno qué días están previstos intercambios de idiomas o actuaciones de monologuistas, o también escuchar la música que suena en el local.
Está bastante cerca de la Plaza Mayor, y tiene una decoración soberbia (paredes empapeladas con partituras, bicicletas colgando del techo, cuadros, chapas, monedas, ...); además el trato es muy amable. Los platos, sin ser demasiado caros, son abundantes y muy bien preparados.
Además, en su página web se puede enterar uno qué días están previstos intercambios de idiomas o actuaciones de monologuistas, o también escuchar la música que suena en el local.
viernes, 12 de septiembre de 2008
¿Qué hemos aprendido?
lunes, 8 de septiembre de 2008
Jethro Tull - Tour 2008
Ahora que ya no me queda más baba por caer, y ya habiendo curado el éxtasis sonoro con el aburrimiento de la carretera en el viaje de regreso, intentaré cargarme de objetividad para describir los dos conciertos a los que he podido asistir, en Alcorcón el sábado y en Salamanca ayer, de la banda Jethro Tull, que celebra con una gira mundial sus 40 años.
Puedo afirmar que en ninguno de los dos conciertos la banda ha defraudado a los cientos de tullianos allí reunidos (es difícil dar una cifra; en Alcorcón nos dijeron que éramos 15000 y en Salamanca la Plaza Mayor estaba a rebosar). Y no lo digo sólo yo. Hay que decir que las condiciones del escenario en Alcorcón no eran las mejores: un campo de fútbol de tierra bastante cutre y un escenario pequeño, como corresponde a las fiestas de un pueblo. Pese a ello, el sonido fue mucho mejor de lo esperado, sin duda gracias a la mano de James Anderson, hijo de Ian Anderson, que se encarga de todos los preparativos y ajustes de sonido antes de cada concierto.
La banda se presentó con un nuevo bajo y un nuevo teclista. Ambos conciertos fueron en la misma línea con ligeras variaciones; el de Salamanca fueron menos canciones, pero de las más míticas hicieron versiones más largas. En general, se puede decir que la banda sigue en plena forma y con su habitual sentido del humor. Combinaron temas muy conocidos con otros menos conocidos, pero cañeros.
Algunas de mis impresiones:
David Goodier, el nuevo bajo, no sólo es mucho más expresivo que el anterior (cosa que no era muy difícil), sino que además ha dado muestras de su virtuosismo y personalidad, llenando en ocasiones el escenario tanto como el propio Ian, Martin o Doane.
John O'Hara, el nuevo teclista, no lo ha hecho mal, pero se echó en falta el papel protagonista que este instrumento solía tener en la banda. Apenas en un par de canciones, cuando los demás instrumentos "callaron", el teclado se dejó notar. Una de ellas fue, cómo no, el comienzo de Locomotive Breath, donde O'Hara dejó claro que también sabe "hacer virguerías".
Doane Perry, el batería, ha estado sencillamente soberbio. Brutal el solo de batería que se marcó en Dharma For One, que nos hizo preguntarnos a los presentes si ese hombre tiene sólo dos brazos y dos piernas. Y también brutal su aportación en Locomotive Breath, de la que hasta ahora nunca había oído una versión tan cañera (y aquí incluyo también versiones como la de Helloween). También hizo los coros de Heavy Horses.
Martin Lancelot Barre, el guitarrista, ha estado especialmente destacado. En los últimos años está cobrando cada vez más protagonismo dentro de la banda, merecido por otro lado al ser el único que se mantiene en ella junto a Ian desde su origen. Es notoria su humildad y timidez fuera del escenario; en cambio cuando se sube a él... En Salamanca sobre todo, se ha desmelenado y se le ha visto disfrutar mientras nos hacía disfrutar.
Ian Scott Anderson, el cantante, flautista, guitarrista, harmonicista, humorista, agitador de masas, ..., el alma del grupo. Empezaré por lo único que se puede decir de él negativo, lo que todos sabemos: no tiene la voz de cuando tenía treinta años. Normal. Pero sí diré que en mi opinión (y la de algunos fans más), ha mejorado su voz en los últimos 5 años, signo de que ha superado los problemas que tenía, o ha elegido un repertorio más adecuado. En todo lo demás, ha estado simplemente excepcional, con su habitual maestría a la flauta y con su tremendo sentido del humor. Momento estelar de su discurso cuando dedicó Too Old To Rock And Roll But Too Young To Die a Mick Jagger, o cuando recordó con asombro aquel galardón que recibió la banda como mejor grupo "Heavy Metal", o también cuando introdujo Bourée como una canción que Bach enseñó a Martin Barre cuando se iban de copas en el siglo XVII, "when men where men". En lo musical, por supuesto, fabuloso, y de forma física enorme, moviéndose continuamente por el escenario, saltando y bailando mientras tocaba, y tocando sobre una pierna..., todo un atleta de 61 años.
Puedo afirmar que en ninguno de los dos conciertos la banda ha defraudado a los cientos de tullianos allí reunidos (es difícil dar una cifra; en Alcorcón nos dijeron que éramos 15000 y en Salamanca la Plaza Mayor estaba a rebosar). Y no lo digo sólo yo. Hay que decir que las condiciones del escenario en Alcorcón no eran las mejores: un campo de fútbol de tierra bastante cutre y un escenario pequeño, como corresponde a las fiestas de un pueblo. Pese a ello, el sonido fue mucho mejor de lo esperado, sin duda gracias a la mano de James Anderson, hijo de Ian Anderson, que se encarga de todos los preparativos y ajustes de sonido antes de cada concierto.
La banda se presentó con un nuevo bajo y un nuevo teclista. Ambos conciertos fueron en la misma línea con ligeras variaciones; el de Salamanca fueron menos canciones, pero de las más míticas hicieron versiones más largas. En general, se puede decir que la banda sigue en plena forma y con su habitual sentido del humor. Combinaron temas muy conocidos con otros menos conocidos, pero cañeros.
Algunas de mis impresiones:
David Goodier, el nuevo bajo, no sólo es mucho más expresivo que el anterior (cosa que no era muy difícil), sino que además ha dado muestras de su virtuosismo y personalidad, llenando en ocasiones el escenario tanto como el propio Ian, Martin o Doane.
John O'Hara, el nuevo teclista, no lo ha hecho mal, pero se echó en falta el papel protagonista que este instrumento solía tener en la banda. Apenas en un par de canciones, cuando los demás instrumentos "callaron", el teclado se dejó notar. Una de ellas fue, cómo no, el comienzo de Locomotive Breath, donde O'Hara dejó claro que también sabe "hacer virguerías".
Doane Perry, el batería, ha estado sencillamente soberbio. Brutal el solo de batería que se marcó en Dharma For One, que nos hizo preguntarnos a los presentes si ese hombre tiene sólo dos brazos y dos piernas. Y también brutal su aportación en Locomotive Breath, de la que hasta ahora nunca había oído una versión tan cañera (y aquí incluyo también versiones como la de Helloween). También hizo los coros de Heavy Horses.
Martin Lancelot Barre, el guitarrista, ha estado especialmente destacado. En los últimos años está cobrando cada vez más protagonismo dentro de la banda, merecido por otro lado al ser el único que se mantiene en ella junto a Ian desde su origen. Es notoria su humildad y timidez fuera del escenario; en cambio cuando se sube a él... En Salamanca sobre todo, se ha desmelenado y se le ha visto disfrutar mientras nos hacía disfrutar.
Ian Scott Anderson, el cantante, flautista, guitarrista, harmonicista, humorista, agitador de masas, ..., el alma del grupo. Empezaré por lo único que se puede decir de él negativo, lo que todos sabemos: no tiene la voz de cuando tenía treinta años. Normal. Pero sí diré que en mi opinión (y la de algunos fans más), ha mejorado su voz en los últimos 5 años, signo de que ha superado los problemas que tenía, o ha elegido un repertorio más adecuado. En todo lo demás, ha estado simplemente excepcional, con su habitual maestría a la flauta y con su tremendo sentido del humor. Momento estelar de su discurso cuando dedicó Too Old To Rock And Roll But Too Young To Die a Mick Jagger, o cuando recordó con asombro aquel galardón que recibió la banda como mejor grupo "Heavy Metal", o también cuando introdujo Bourée como una canción que Bach enseñó a Martin Barre cuando se iban de copas en el siglo XVII, "when men where men". En lo musical, por supuesto, fabuloso, y de forma física enorme, moviéndose continuamente por el escenario, saltando y bailando mientras tocaba, y tocando sobre una pierna..., todo un atleta de 61 años.
Espero que duren muchos años más.
domingo, 7 de septiembre de 2008
Y otro concierto!!!
¡¡¡Hoy toca en Salamanca!!!
Digo lo mismo que ayer; este post es programado, pero mañana os contaré qué tal. Esta vez es en la Plaza Mayor de Salamanca y también es gratuito. Son estos los dos únicos conciertos que los Jethro Tull darán este año en España. A pesar de la acústica previsiblemente no muy buena de los conciertos, confío en que la segunda banda más antigua en activo (después de sus satánicas majestades) seguirá en forma y no nos defraudará. Al fin y al cabo seguirán siendo "too old to rock and roll but too young to die".
El experimento de la doble ranura
Corría el año 1801 cuando el polifacético Thomas Young hizo pasar un rayo de luz a través de dos rendijas paralelas, generando un patrón de bandas en una pantalla al otro lado, y demostrando así la naturaleza ondulatoria de la luz. Probablemente, a pesar de la disquisición histórica del momento entre partícula y onda, no imaginaba Young la trascendencia que su experimento iba a tener, no sólo respecto a la naturaleza de la luz, sino la de la misma materia y las ondas. Al igual que la luz, otras partículas cuánticas poseen una inseparabilidad absoluta entre su naturaleza ondulatoria y su naturaleza corpuscular. Las implicaciones que esto conlleva son cruciales a la hora de entender de qué está hecha la materia. El siguiente vídeo explica de una manera clara y divertida todos estos interesantes conceptos:
sábado, 6 de septiembre de 2008
Concierto!!!
Jethro Tull y Gwendal. Dos grandes bandas, dos clásicos. Sé que me pueden los colores, pero los Jethro Tull son de lo mejorcito que queda en activo. Espero que el hecho de ser gratis y al aire libre no perjudique demasiado al espectáculo. El lunes os contaré qué tal ha ido (este es un post programado).
www.chesstempo.com
Ya mencioné esta página cuando hablé de www.chess.com, pero ahora que llevo un tiempo utilizándola, puedo reafirmarme en mi opinión de que es la mejor herramienta que conozco para entrenar táctica en ajedrez.
La forma de trabajar es muy simple. Sólo se trata de resolver problemas tácticos, aunque la página también te saca estadísticas y gráficas de tu rating. Lo que hace de este sitio el mejor, desde mi punto de vista, es la calidad (y cantidad) de los problemas. Después de haber resuelto unos 750 de los más de 15000 existentes, puedo decir que los ejercicios son de un nivel adecuado (se seleccionan por dificultad de acuerdo al nivel de cada uno) y que no he encontrado ni un solo fallo en ninguno de ellos.
Resolviendo problemas de este tipo aprendes a pensar al darte cuenta de muchos fallos. Por ejemplo, es típico el caso de pensar que una línea es correcta y no serlo (te obligan a pensar más) o el caso de pensar que hay 2 jugadas buenas, pero después descubres que una de ellas tenía una refutación. Sin duda, para el que quiera mejorar y se lo tome en serio, un muy buen recurso.
viernes, 5 de septiembre de 2008
Spore
¡¡Ya está aquí!! ¡¡Ya llega!! ¡¡Por fin!!
El momento que muchos estábamos esperando. Falta 1 día y 22 horas para el lanzamiento oficial de Spore, que como sabréis es... simplemente el juego definitivo. Afortunadamente antes de que acabemos con nuestro planeta disponemos de la posibilidad de crear una nueva civilización para conquistar otras galaxias.
Para abrir boca, en este vídeo podéis ver un trailer de la fase espacial del juego. Promete.
Para aquellos que ya hayáis viciado con el Creature Creator, tal vez os interese saber que en este sitio podéis diseñar y comprar camisetas con vuestras criaturas. Desde luego hasta ahora han sabido venderlo muy bien; dentro de unos días podremos saber si el juego está a la altura de sus elevadísimas expectativas.
jueves, 4 de septiembre de 2008
Genio de genios
"Si von Neumann dice que es obvio, podrás demostrarlo en tres meses, si eres un genio."
Ralph Philip Boas
Ralph Philip Boas
martes, 2 de septiembre de 2008
Va a comenzar el gran experimento
Ya casi queda una semana para que pongan en funcionamiento el primer haz de hadrones en el Gran Colisionador de Hadrones del CERN. Concretamente, desde el 10 de septiembre a las 9 de la mañana se podrá seguir en directo el webcast que para ello han creado en este enlace.
Que el experimento acabe en tragedia/catástrofe/destrucción masiva del universo que conocemos, como sugieren algunas teorías, es una posibilidad como cualquier otra. No en vano se pretenden estudiar "cosas" que podrían explicar algunas cuestiones fundamentales del Universo (como ciertas partículas de las que poco o nada se sabe o por qué la fuerza de gravedad es tan débil respecto a las demás), y cuando se estudia algo que se desconoce siempre se está corriendo el riesgo de "jugar con fuego".
Este vídeo es una explicación bastante visual de qué hace el colisionador y cuál es el supuesto riesgo.
Los que sustentan las teorías alarmistas proponen que no se ponga en marcha el colisionador hasta que nos aseguremos de que es seguro. Si el experimento nos va a permitir entender eso que desconocemos y que supone un riesgo, la pregunta es: ¿cómo vamos a saber que es seguro sin probarlo? ¿Hasta dónde estamos dispuestos a arriesgarnos por aprender?... Es el eterno debate; ya se sabe que la curiosidad mató al gato.
Sin embargo, no nos alarmemos. Como es lógico, el CERN ha llevado a cabo estudios sobre la posibilidad de que se produzcan microagujeros negros inestables, monopolos magnéticos, strangelets y demás amenazas, llegando a la conclusión de que, aunque efectivamente nadie puede asegurar que no se vayan a producir, la Naturaleza ya ha producido el equivalente a más de un millón de colisiones y la Tierra sigue existiendo... Lo mismo dicen del Sol y del resto de estrellas y galaxias (aunque cabría preguntarse si no habrán "dejado de existir" muchas más que ya no vemos).
Esperemos que todo vaya bien y que podamos aprender nuevas lecciones acerca del Universo que nos rodea. Y si algo sale mal... ¿quién sabe?, tal vez en otra galaxia muy muy lejana, algún observador nos conceda el equivalente a un premio Darwin.
Que el experimento acabe en tragedia/catástrofe/destrucción masiva del universo que conocemos, como sugieren algunas teorías, es una posibilidad como cualquier otra. No en vano se pretenden estudiar "cosas" que podrían explicar algunas cuestiones fundamentales del Universo (como ciertas partículas de las que poco o nada se sabe o por qué la fuerza de gravedad es tan débil respecto a las demás), y cuando se estudia algo que se desconoce siempre se está corriendo el riesgo de "jugar con fuego".
Este vídeo es una explicación bastante visual de qué hace el colisionador y cuál es el supuesto riesgo.
Los que sustentan las teorías alarmistas proponen que no se ponga en marcha el colisionador hasta que nos aseguremos de que es seguro. Si el experimento nos va a permitir entender eso que desconocemos y que supone un riesgo, la pregunta es: ¿cómo vamos a saber que es seguro sin probarlo? ¿Hasta dónde estamos dispuestos a arriesgarnos por aprender?... Es el eterno debate; ya se sabe que la curiosidad mató al gato.
Sin embargo, no nos alarmemos. Como es lógico, el CERN ha llevado a cabo estudios sobre la posibilidad de que se produzcan microagujeros negros inestables, monopolos magnéticos, strangelets y demás amenazas, llegando a la conclusión de que, aunque efectivamente nadie puede asegurar que no se vayan a producir, la Naturaleza ya ha producido el equivalente a más de un millón de colisiones y la Tierra sigue existiendo... Lo mismo dicen del Sol y del resto de estrellas y galaxias (aunque cabría preguntarse si no habrán "dejado de existir" muchas más que ya no vemos).
Esperemos que todo vaya bien y que podamos aprender nuevas lecciones acerca del Universo que nos rodea. Y si algo sale mal... ¿quién sabe?, tal vez en otra galaxia muy muy lejana, algún observador nos conceda el equivalente a un premio Darwin.
Mi método para sumas infinitas
Hace unos días, hablando con un colega acerca del fractal de copo de nieve, recordé que se trata de una figura de área finita y perímetro infinito (paradójicamente), y me pregunté cuál será su área. Haciendo unos sencillos cálculos me topé con la suma infinita:
A=1+3/9+12/81+48/729+...
suponiendo que el área del triángulo original es 1. En esa serie cada término a partir del tercero es exactamente 4/9 del término anterior. En esta página podéis ver un método (de hecho el típico) para resolver la suma, pero yo aquí voy a explicar el mío, que aunque no siempre es aplicable, cuando lo es resulta bastante inmediato.
Fijémonos que cada término se puede obtener del anterior de la misma manera, excepto con el primer par, por lo que voy a separar el primer sumando.
A=1+S
donde S=3/9+12/81+48/729+... es la suma que queremos calcular. Como es una suma de infinitos términos y cada uno se obtiene del anterior podemos escribir fácilmente la suma de todos menos el primero a partir de la suma completa:
12/81+48/729+... = (4/9) x (3/9+12/81+48/729+...)
Y aquí está el truco, nos aprovechamos del infinito para establecer que S=3/9+(4/9) x S
Nos queda una sencilla ecuación de la que despejamos S=0'6, por lo que A=1'6, es decir, el área del fractal del copo de nieve es 1'6 veces la del triángulo original.
Probemos nuestro método con otra suma bien conocida:
S=1/2+1/4+1/8+1/16+...
Todos sabemos, o deberíamos saber, que esa suma da como resultado 1, cosa que se puede demostrar de muchas maneras (interesante la refutación de la paradoja de la piedra de Zenón). Nosotros vamos a usar nuestro método. Recordemos: se trata de descartar el primer sumando y escribir los demás en función de la propia suma completa. Veamos... la suma S es 1/2 más... la propia suma S dividida entre 2. Así de sencillo:
S=1/2+S/2
De ahí se deduce, evidentemente, que S=1
Un último ejemplo, para acabar. Según la Wikipedia, el número áureo se puede obtener de la siguiente fracción continua:
¿Será verdad? También aquí podemos utilizar nuestro método, pues la suma S es igual a uno más uno partido por... la propia suma:
S=1+1/S
Resolviendo la ecuación de segundo grado resultante, efectivamente obtenemos que S=(raiz(5)+1)/2, que es la definición de número áureo.
Espero que os pueda servir de algo "mi método".
A=1+3/9+12/81+48/729+...
suponiendo que el área del triángulo original es 1. En esa serie cada término a partir del tercero es exactamente 4/9 del término anterior. En esta página podéis ver un método (de hecho el típico) para resolver la suma, pero yo aquí voy a explicar el mío, que aunque no siempre es aplicable, cuando lo es resulta bastante inmediato.
Fijémonos que cada término se puede obtener del anterior de la misma manera, excepto con el primer par, por lo que voy a separar el primer sumando.
A=1+S
donde S=3/9+12/81+48/729+... es la suma que queremos calcular. Como es una suma de infinitos términos y cada uno se obtiene del anterior podemos escribir fácilmente la suma de todos menos el primero a partir de la suma completa:
12/81+48/729+... = (4/9) x (3/9+12/81+48/729+...)
Y aquí está el truco, nos aprovechamos del infinito para establecer que S=3/9+(4/9) x S
Nos queda una sencilla ecuación de la que despejamos S=0'6, por lo que A=1'6, es decir, el área del fractal del copo de nieve es 1'6 veces la del triángulo original.
Probemos nuestro método con otra suma bien conocida:
S=1/2+1/4+1/8+1/16+...
Todos sabemos, o deberíamos saber, que esa suma da como resultado 1, cosa que se puede demostrar de muchas maneras (interesante la refutación de la paradoja de la piedra de Zenón). Nosotros vamos a usar nuestro método. Recordemos: se trata de descartar el primer sumando y escribir los demás en función de la propia suma completa. Veamos... la suma S es 1/2 más... la propia suma S dividida entre 2. Así de sencillo:
S=1/2+S/2
De ahí se deduce, evidentemente, que S=1
Un último ejemplo, para acabar. Según la Wikipedia, el número áureo se puede obtener de la siguiente fracción continua:
¿Será verdad? También aquí podemos utilizar nuestro método, pues la suma S es igual a uno más uno partido por... la propia suma:S=1+1/S
Resolviendo la ecuación de segundo grado resultante, efectivamente obtenemos que S=(raiz(5)+1)/2, que es la definición de número áureo.
Espero que os pueda servir de algo "mi método".
domingo, 31 de agosto de 2008
Acertijos I
Celebrando el día del blog, inauguro una nueva sección: acertijos. Los problemas que propondré siempre se van a poder resolver con alguna de las herramientas o trucos explicados anteriormente en el blog. De cada vez dejaré 3 problemillas crecientes en dificultad (según mi opinión). La idea es que os sirvan a vosotros para mantener la mente ágil, y a mí ... para tener algún comentario en el blog; os ruego que escribáis vuestras hipótesis, dudas o respuestas en los comentarios.
Aquí van los acertijos de hoy:
Fácil: ¿Es posible escoger 1005 números del conjunto {1,2,3,...,2008} sin que haya 2 de ellos que sumen 2009?
Medio: Probar que en una reunión de 6 personas, o bien hay 3 que se conocen entre sí o bien hay 3 que no se conocen entre sí. (NOTA: si A conoce a B, entonces B conoce a A)
Difícil: ¿Existirá algún múltiplo de 2009 que se escriba sólo con unos?
PISTA: La única "herramienta" que hemos visto hasta ahora en el blog es el principio del palomar, así que se pueden resolver todos con él (y con un poco de pensar).
BlogDay 2008
Parece ser que hoy se celebra internacionalmente el día del blog, dado que 31/08 escrito de cierta manera puede parecerse a la palabra Blog. El caso es que existe en el BlogDay la tradición de que cada blog publique una entrada donde enlace a otros 5 blogs que considera interesantes, preferiblemente de otra cultura, punto de vista o posición. Una iniciativa sin duda interesante para, como dicen ellos, "spreading the word".
Pues aquí van mis 5 blogs seleccionados, los cuales he descubierto este año (excepto el primero):
JOTMAN - Con una excelente crítica internacional desde hace años, así como un premio de Reporteros sin Fronteras en su haber, el autor de este blog viaja a los puntos calientes del planeta para informar in situ de algunas de las crisis más graves que sufre el mundo.- Thailand: Krabi airport closed, Phuket closed
- Nepal source of massive flood in Bihar, India
- Who won the Georgia-Russia war?
Historias de la ciencia - Entretenido blog que trata de eso, historias de la ciencia, combinando reseñas históricas de personajes o hitos claves con anécdotas más modernas, siempre en un estilo desenfadado y divulgativo.Eliax Blog - "Para mentes curiosas", reza su portada. Aglomera un montón (pero un montón) de curiosidades y novedades de la actualidad tecnológica. Muy interesante.- Google construyendo cable submarino entre EEUU, Asia, África
- Ilusiones Ópticas en el arte
- Descifrado: Por qué es tan difícil aplastar una mosca...
Navegapolis.net - Blog de Juan Palacio dedicado a la gestión en empresas de desarrollo de software, ingeniería del software y TI en general.- Los conocimientos que andan buscando las empresas TIC
- Tesis sobre Extreme Programming
- 21 posturas para hacer el amor con tus clientes
Get Rich Slowly - Bajo este título spamoide se esconde un interesante blog donde la gente comparte trucos y consejos de toda clase (pero de toda clase) para ahorrar dinero.- The GRS Garden Project: August Update
- How to Win the Lottery
- Building a Better Budget: Think Yearly, Not Monthly
¡Feliz día del blog!
sábado, 30 de agosto de 2008
La paradoja de Abilene
La semana pasada contamos cómo la paradoja de Galileo nos enseñó a entender un poco más por qué el infinito es tan difícil de entender a veces, y cómo Cantor la utilizó cuando desarrolló su Teoría de Conjuntos. Hoy propongo cambiar completamente de registro para hablar de una paradoja de economía (según la clasificación de Wikipedia), aunque yo la clasificaría dentro del grupo de paradojas del comportamiento social humano.
La paradoja viene a decir que en ocasiones, normalmente en situaciones críticas, un grupo de personas pueden tomar una decisión como grupo que ninguno de los individuos quiere tomar, siendo por otro lado una decisión mala. La paradoja fue enunciada en 1988 por Jerry B. Harvey en su libro Meditations on Management. Podéis leer la anécdota descrita por Harvey aquí. Básicamente nos habla de una familia que decide hacer un viaje que a ninguno le apetece, porque cada uno de los individuos piensa que los demás quieren hacerlo. El sitio al que viajan es Abilene.
Este tipo de comportamiento colectivo se relaciona con la tendencia que tienen los seres humanos a no ir en contra del resto del grupo. En los equipos de trabajo (y especialmente en las tomas de decisiones) debería intentar evitarse este conformismo en los integrantes, que podría dar lugar, en virtud de la paradoja, a una decisión mala. La paradoja de Abilene nos enseña que hay que tener en cuenta algo más que los votos de los individuos en una decisión grupal, pues estos pueden estar afectados por este "mal social". Algunos consultores utilizan la técnica de preguntarse "¿Estamos yendo a Abilene?" para incentivar la sinceridad de todos los individuos a la hora de mostrar su conformidad o no con una decisión.
La paradoja viene a decir que en ocasiones, normalmente en situaciones críticas, un grupo de personas pueden tomar una decisión como grupo que ninguno de los individuos quiere tomar, siendo por otro lado una decisión mala. La paradoja fue enunciada en 1988 por Jerry B. Harvey en su libro Meditations on Management. Podéis leer la anécdota descrita por Harvey aquí. Básicamente nos habla de una familia que decide hacer un viaje que a ninguno le apetece, porque cada uno de los individuos piensa que los demás quieren hacerlo. El sitio al que viajan es Abilene.
Este tipo de comportamiento colectivo se relaciona con la tendencia que tienen los seres humanos a no ir en contra del resto del grupo. En los equipos de trabajo (y especialmente en las tomas de decisiones) debería intentar evitarse este conformismo en los integrantes, que podría dar lugar, en virtud de la paradoja, a una decisión mala. La paradoja de Abilene nos enseña que hay que tener en cuenta algo más que los votos de los individuos en una decisión grupal, pues estos pueden estar afectados por este "mal social". Algunos consultores utilizan la técnica de preguntarse "¿Estamos yendo a Abilene?" para incentivar la sinceridad de todos los individuos a la hora de mostrar su conformidad o no con una decisión.
1984
Después de mucho tiempo esperando, hoy por fin he visto 1984, la adaptación al cine (en 1984, casualmente) de la novela de George Orwell que lleva el mismo título.
Título: 1984Director: Michael Radford
Año: 1984
Reparto:
John Hurt
Richard Burton
Suzanna Hamilton
Argumento: Winston Smith (John Hurt) es un trabajador del Ministerio de la Verdad de una sociedad distópica, y se dedica a rescribir la Historia e inventar héroes. Toda la política se resume en el Gran Hermano, a quien todo el mundo debe obediencia. Cualquier desvío de las doctrinas del Gran Hermano supone un crimen, empezando por la sola idea de llevarle la contraria o tener iniciativa para pensar por cuenta de uno mismo, lo cual constituye el crimen más básico: el llamado crimen mental. Para perseguir a los "criminales mentales" existe la policía del pensamiento, que no se anda con miramientos a la hora de corregir a los criminales: primero les lava el cerebro (mediante torturas) hasta que reconocen amar al Gran Hermano y haber vuelto a la "senda correcta", y después los ejecutan.
Por supuesto el protagonista, como en todas las historias de este tipo, se acaba poniendo de alguna manera contra el sistema. En este caso, sin revelar más del argumento, diré que como se puede suponer acaba convirtiéndose en un "criminal mental", cuando se cuestiona por qué las cosas son como son y por qué no se siente libre.
Por supuesto el protagonista, como en todas las historias de este tipo, se acaba poniendo de alguna manera contra el sistema. En este caso, sin revelar más del argumento, diré que como se puede suponer acaba convirtiéndose en un "criminal mental", cuando se cuestiona por qué las cosas son como son y por qué no se siente libre.
Valoración: El argumento es genial, para quien le gusta este tipo de historias, y es rico en detalles descriptivos que nos permiten comprender cómo piensa la gente en esa hipotética sociedad. Por otro lado, en las casi 2 horas de película no hay nada de acción, con lo que la atención del espectador se mantiene despierta solamente de manera activa, a través de diálogos y monólogos profundos, en ocasiones difíciles de comprender a la primera, lo que hace que sea un poco tediosa. Por ello, si eres un friki como yo y estás despierto y preparado para darle al coco, la película te gustará bastante y te dará que pensar. Si no cumples estos requisitos, no pierdas el tiempo viéndola: es probable que te duerma.
viernes, 29 de agosto de 2008
No nos olvidemos de poner la semilla...
"El que aprende y aprende y no practica lo que aprende, es como el que ara y ara y nunca siembra."
Platón
Platón
Mejora tu productividad
...O al menos conócela, podríamos decir. Este es el objetivo de RescueTime, una interesante aplicación que te permitirá llevar de forma automática un log del tiempo que dedicas a cada actividad (programa, página web, ...) en tu ordenador. En la página web se encargan de generarte gráficas de barras y líneas para que veas cómo ha sido tu productividad de la semana o del mes, en qué inviertes más tiempo y en qué menos, ... Se pueden definir objetivos y generar alertas (te manda un mail) en caso de que no se cumplan.
www.chess.com
Tan fácil como teclear www.chess.com en el navegador. Este sitio hará las delicias de los amantes del ajedrez, llegando desde mi punto de vista a ser una página de referencia como lo era hasta ahora www.chessgames.com. Se pueden explorar aperturas, resolver problemas, etc..., lo típico. Pero además, la página está claramente orientada a jugar partidas por correo, pudiendo jugar torneos y partidas a diferentes ritmos. También tiene su parte de juego en tiempo real, así como una sección para jugar contra una máquina con la que puedes practicar (si tienes más de 2000 ELO no pierdas el tiempo, le ganarás fácil).
Por último, aprovecho la entrada para enlazar con otro sitio que me ha sorprendido gratamente, chesstempo.com, el mejor sitio que conozco para entrenar táctica.
jueves, 28 de agosto de 2008
Bendita ignorancia
"Por la ignorancia nos equivocamos, y por las equivocaciones aprendemos."
Proverbio Romano
Proverbio Romano
Se admiten apuestas
Ayer tuve ocasión de pasarme por el edificio de la Facultad de Física de Ourense, y me encontré con un bonito mural (en el pasillo de la primera planta, para los que le quede a mano) que resume grandes personajes e hitos de la historia de la Ciencia (centrado mayormente, pero no todo, en la Física). Entre esos personajes pude ver a Sheldon Lee Glashow, por su teoría electrodébil que le valió el Nobel en 1979, junto a Steven Weinberg y Abdus Salam.
Entonces me pregunté: ¿será en honor a Glashow que nuestro ídolo se llama Sheldon? De ser así, yo apostaría a que Leonhard toma su nombre del gran Euler.
¿Pero y los otros dos?... Ahí queda eso; se admiten apuestas.
Entonces me pregunté: ¿será en honor a Glashow que nuestro ídolo se llama Sheldon? De ser así, yo apostaría a que Leonhard toma su nombre del gran Euler.
¿Pero y los otros dos?... Ahí queda eso; se admiten apuestas.
miércoles, 27 de agosto de 2008
Calendario lunar
La semana que viene comienza el mes de Ramadán musulmán, lo cual nos recuerda que el calendario árabe es diferente al nuestro. Toma como base el tiempo que hay entre una luna nueva y la siguiente, es decir, 29 días y medio. Por ello, el año musulmán tiene 12 meses, cinco de ellos de 29 días y los demás de 30, haciendo un total de 354, días es decir, con 11 días de desfase respecto al año solar. Por ello, los meses del calendario árabe se van desplazando cada año a lo largo de las estaciones (en el antiguo calendario pre-islámico se añadía un mes cada 3 años a fin de corregir este desfase; hoy en día se abandonó esta práctica).
El mes de Ramadán, el noveno del calendario árabe, conmemora la primera revelación de Alá a Mahoma. Durante ese mes, todos los que han llegado a la pubertad han de abstenerse de comer, beber, fumar, usar perfumes y tener relaciones sexuales durante las horas diurnas, es decir, desde que sale el Sol hasta que se pone y empieza un nuevo día, ya que para los musulmanes los días empiezan a contarse después de la puesta del Sol, "cuando ya no es posible distinguir un hilo blanco de un hilo negro".
Los próximos años serán especialmente duros, ya que el mes de Ramadán, que cada año (solar) empieza unos 10 u 11 días antes que el anterior, está empezando a celebrarse en los meses calurosos del verano. Los devotos musulmanes valoran en gran medida el entrenamiento que proporciona como disciplina espiritual y como muestra del triunfo de la mente sobre la materia.
Fuente: WebIslam
El mes de Ramadán, el noveno del calendario árabe, conmemora la primera revelación de Alá a Mahoma. Durante ese mes, todos los que han llegado a la pubertad han de abstenerse de comer, beber, fumar, usar perfumes y tener relaciones sexuales durante las horas diurnas, es decir, desde que sale el Sol hasta que se pone y empieza un nuevo día, ya que para los musulmanes los días empiezan a contarse después de la puesta del Sol, "cuando ya no es posible distinguir un hilo blanco de un hilo negro".
Los próximos años serán especialmente duros, ya que el mes de Ramadán, que cada año (solar) empieza unos 10 u 11 días antes que el anterior, está empezando a celebrarse en los meses calurosos del verano. Los devotos musulmanes valoran en gran medida el entrenamiento que proporciona como disciplina espiritual y como muestra del triunfo de la mente sobre la materia.
Fuente: WebIslam
Mr Pip
Título: Mister PipAutor: Lloyd Jones
Año: 2007
ISBN: 978-0-7195-6994-4
Páginas: 219
Argumento: Matilda es una joven niña de Bougainville, una isla tropical que se ve salpicada por el horror del estallido de una guerra civil. Mr Watts, la única persona blanca, se ofrece a ser el profesor de la pequeña escuela en la que el único libro de texto es Great Expectations, de Dickens, "un libro extraordinario".
Valoración: Tuve la suerte de encontrarme este libro en un aeropuerto británico este verano, por lo que lo he comprado en inglés. Aunque todavía no lo he terminado, ya estoy a punto de devorar las últimas páginas y puedo decir que el inglés de este libro se entiende bastante bien (la catalogaría de novela infantil), pues es más sencillo que el del propio Great Expectations. La historia me está encantando (también puede tener que ver que soy un enamorado de Great Expectations), no sólo por su argumento de historia bonita/triste, sino por lo poético, encantador y sorprendente del relato desde la visión infantil de la protagonista. Por otro lado, puedo intuir un final mágico (y las críticas que he leído lo confirman).
En definitiva, una historia cautivadora que profundiza en la naturaleza humana de los personajes y de la que se pueden extraer algunas moralejas. No es imprescindible haber leído Great Expectations, pero aunque son completamente diferentes (en argumento, lenguaje y longitud), si te gusta uno seguramente te gustará el otro.
Actualización (5-10-2008): Ya he terminado de leerlo.
Valoración: Tuve la suerte de encontrarme este libro en un aeropuerto británico este verano, por lo que lo he comprado en inglés. Aunque todavía no lo he terminado, ya estoy a punto de devorar las últimas páginas y puedo decir que el inglés de este libro se entiende bastante bien (la catalogaría de novela infantil), pues es más sencillo que el del propio Great Expectations. La historia me está encantando (también puede tener que ver que soy un enamorado de Great Expectations), no sólo por su argumento de historia bonita/triste, sino por lo poético, encantador y sorprendente del relato desde la visión infantil de la protagonista. Por otro lado, puedo intuir un final mágico (y las críticas que he leído lo confirman).
En definitiva, una historia cautivadora que profundiza en la naturaleza humana de los personajes y de la que se pueden extraer algunas moralejas. No es imprescindible haber leído Great Expectations, pero aunque son completamente diferentes (en argumento, lenguaje y longitud), si te gusta uno seguramente te gustará el otro.
Actualización (5-10-2008): Ya he terminado de leerlo.
Google Notepad
Hace un par de días que empecé a utilizar Google Notebook. Esta herramienta te permite crear/almacenar notas mientras navegas por la web, para consultarlas más adelante. Es ideal para procrastinadores como yo, ya que una vez instalado el plugin para Firefox, es muy cómodo de usar, y te permite seleccionar texto y/o imágenes de cualquier sitio web e incorporarlos a una nueva nota, así como poner comentarios y etiquetas a las notas. Lo de las etiquetas es especialmente útil para explorar posteriormente las notas por categorías. En el Firefox se instala como una práctica cajita minimizable situada debajo a la derecha:
También se pueden explorar y manejar todas las notas desde la propia página de Google Notebook.
También se pueden explorar y manejar todas las notas desde la propia página de Google Notebook.
martes, 26 de agosto de 2008
Mathematical pi
Genial este vídeo/canción dedicado a nuestro queridísimo pi:
Pero el vídeo anterior sólo llega hasta el primer estribillo. Si os ha gustado, en la web de Antoni "Ton" Chan podéis encontrar la canción completa en mp3, así como su letra.
Pero el vídeo anterior sólo llega hasta el primer estribillo. Si os ha gustado, en la web de Antoni "Ton" Chan podéis encontrar la canción completa en mp3, así como su letra.
Vía: Microsiervos
¿Quién fue Doppler?
Todos hemos oído hablar del efecto Doppler, ¿verdad? Si alguno no sabe de qué estamos hablando, Sheldon se encargará de resolver todas sus dudas:
Pero, ¿quién fue Doppler?
Pues bien, Christian Andreas Doppler fue un matemático y astrónomo de origen austríaco que vivió en la primera mitad del siglo XIX. Su gran ingenio y capacidad creativa, dignas del mismísimo Inventor, se pueden malamente resumir en la siguiente valoración del admirable Bolzano:
"El profesor Doppler a lo largo de varias semanas me ha excitado con sus ideas, cada una más brillante que la anterior. Me veo obligado a reflexionar sobre ellas día y noche"
Entre todas las ideas, en ocasiones visionarias, de Doppler, pasó a la posteridad el efecto que lleva su nombre. En su obra "Sobre el color de la luz en estrellas binarias y otros astros", de 1842, Doppler vaticinó (¡con éxito!) que algún día los astrónomos serían capaces de distinguir en las estrellas dobles cuál se acercaba y cuál se alejaba a la Tierra por diferencias en su color.
Lo curioso es que Doppler desarrolló su teoría sin tener ninguna evidencia que la corroborase, ya que en su época ningún instrumento óptico era capaz de medir diferencias tan pequeñas en el color de las estrellas. Sólo 3 años después se le ocurrió que su efecto podría percibirse mejor aplicado al sonido y, tras una serie de experimentos que involucraban músicos tocando en trenes en movimiento, en 1846 publicó una versión mejorada de su teoría.
Pero, ¿quién fue Doppler?
Pues bien, Christian Andreas Doppler fue un matemático y astrónomo de origen austríaco que vivió en la primera mitad del siglo XIX. Su gran ingenio y capacidad creativa, dignas del mismísimo Inventor, se pueden malamente resumir en la siguiente valoración del admirable Bolzano:
"El profesor Doppler a lo largo de varias semanas me ha excitado con sus ideas, cada una más brillante que la anterior. Me veo obligado a reflexionar sobre ellas día y noche"
Entre todas las ideas, en ocasiones visionarias, de Doppler, pasó a la posteridad el efecto que lleva su nombre. En su obra "Sobre el color de la luz en estrellas binarias y otros astros", de 1842, Doppler vaticinó (¡con éxito!) que algún día los astrónomos serían capaces de distinguir en las estrellas dobles cuál se acercaba y cuál se alejaba a la Tierra por diferencias en su color.
Lo curioso es que Doppler desarrolló su teoría sin tener ninguna evidencia que la corroborase, ya que en su época ningún instrumento óptico era capaz de medir diferencias tan pequeñas en el color de las estrellas. Sólo 3 años después se le ocurrió que su efecto podría percibirse mejor aplicado al sonido y, tras una serie de experimentos que involucraban músicos tocando en trenes en movimiento, en 1846 publicó una versión mejorada de su teoría.
Fuentes:
Answers.com
The MacTutor History of Mathematics archive
Dr James B. Calvert's Personal Page
Wikipedia: 1, 2, 3 y 4
Answers.com
The MacTutor History of Mathematics archive
Dr James B. Calvert's Personal Page
Wikipedia: 1, 2, 3 y 4
lunes, 25 de agosto de 2008
La paradoja de Galileo
Con esta breve reseña histórica pretendo abrir un bloque de posts dedicados a paradojas. En términos generales, una paradoja es un resultado que parece ser cierto a pesar de que contradice nuestros principios. Por ello, las paradojas tienen una importante componente de reto mental, ya que nos obligan a cuestionar nuestras creencias. El pensamiento científico, a lo largo de su historia, se ha enfrentado a diversas paradojas, que nos han hecho rectificar y evolucionar, es decir, aprender.
Corría el año 1636 cuando Galileo Galilei, recluido de por vida en su casa de Florencia debido a sus conocidas ideas copernicanas, hace publicar su último libro justo antes de perder la vista: "Discursos sobre dos nuevas ciencias". Estas ciencias a las que se refiere y que pretende postular son la mecánica y la resistencia de los materiales, que sin bien no ciencias completas, hoy son campos fundamentales de la Física moderna. En este trabajo, Galileo hace algunas afirmaciones acerca del conjunto infinito de los números naturales que resultan ciertamente paradójicas. Podemos resumirlas en las 2 afirmaciones siguientes:
Corría el año 1636 cuando Galileo Galilei, recluido de por vida en su casa de Florencia debido a sus conocidas ideas copernicanas, hace publicar su último libro justo antes de perder la vista: "Discursos sobre dos nuevas ciencias". Estas ciencias a las que se refiere y que pretende postular son la mecánica y la resistencia de los materiales, que sin bien no ciencias completas, hoy son campos fundamentales de la Física moderna. En este trabajo, Galileo hace algunas afirmaciones acerca del conjunto infinito de los números naturales que resultan ciertamente paradójicas. Podemos resumirlas en las 2 afirmaciones siguientes:
- Existen números naturales que son cuadrados perfectos y otros que no, por lo que los cuadrados perfectos son un subconjunto, una parte del conjunto de los números naturales.
- Por cada cuadrado perfecto hay exactamente un número que es su raíz cuadrada, y por cada número hay exactamente otro que es su cuadrado, así que no puede haber más de un tipo que de otro.
La paradoja radica en que estas 2 afirmaciones, que entonces y ahora podemos convencernos de que son absolutamente ciertas, cuestionan el principio básico de la Teoría de Conjuntos de que el todo es mayor que sus partes, porque en este caso hay una parte (el conjunto de los cuadrados perfectos) que sería igual al todo (los números naturales) aun cuando parece imposible al haber elementos en el todo que no están en la parte (los no-cuadrados perfectos).
¿Qué aprendió Galileo de esto? Llegó a la conclusión de que las relaciones de orden (menor, mayor e igual) sólo tienen sentido aplicadas a conjuntos finitos.
Cierto es que en la época de Galileo la Teoría de Conjuntos no estaba todavía desarrollada, y la paradoja ponía en entredicho más bien a la "intuición" de los hombres de ciencia. En el siglo XIX, el gran Georg Cantor desarrolló los fundamentos de la Teoría de Conjuntos que conocemos hoy en día, utilizando en parte las ideas de Galileo. ¿Qué aprendió Cantor de la paradoja de Galileo? Descubrió que las afirmaciones de Galileo eran válidas para el conjunto de los números enteros y el de los racionales. La paradoja le impulsó a investigar las propiedades de los conjuntos infinitos (sin duda nadie los ha estudiado como él) y llegó a la conclusión de que algunos conjuntos infinitos eran mayores que otros.
La paradoja de Galileo, una observación sencilla que aportó su granito de arena al impulso de la investigación y progreso en la Ciencia. Así son las paradojas.
¿Qué aprendió Galileo de esto? Llegó a la conclusión de que las relaciones de orden (menor, mayor e igual) sólo tienen sentido aplicadas a conjuntos finitos.
Cierto es que en la época de Galileo la Teoría de Conjuntos no estaba todavía desarrollada, y la paradoja ponía en entredicho más bien a la "intuición" de los hombres de ciencia. En el siglo XIX, el gran Georg Cantor desarrolló los fundamentos de la Teoría de Conjuntos que conocemos hoy en día, utilizando en parte las ideas de Galileo. ¿Qué aprendió Cantor de la paradoja de Galileo? Descubrió que las afirmaciones de Galileo eran válidas para el conjunto de los números enteros y el de los racionales. La paradoja le impulsó a investigar las propiedades de los conjuntos infinitos (sin duda nadie los ha estudiado como él) y llegó a la conclusión de que algunos conjuntos infinitos eran mayores que otros.
La paradoja de Galileo, una observación sencilla que aportó su granito de arena al impulso de la investigación y progreso en la Ciencia. Así son las paradojas.
Suscribirse a:
Entradas (Atom)
Entradas
